Coordinate System and Shapes
Before we begin programming with p5, we must first channel our eighth grade selves, pull out a piece of graph paper, and draw a line. The shortest distance between two points is a good old fashioned line, and this is where we begin, with two points on that graph paper.
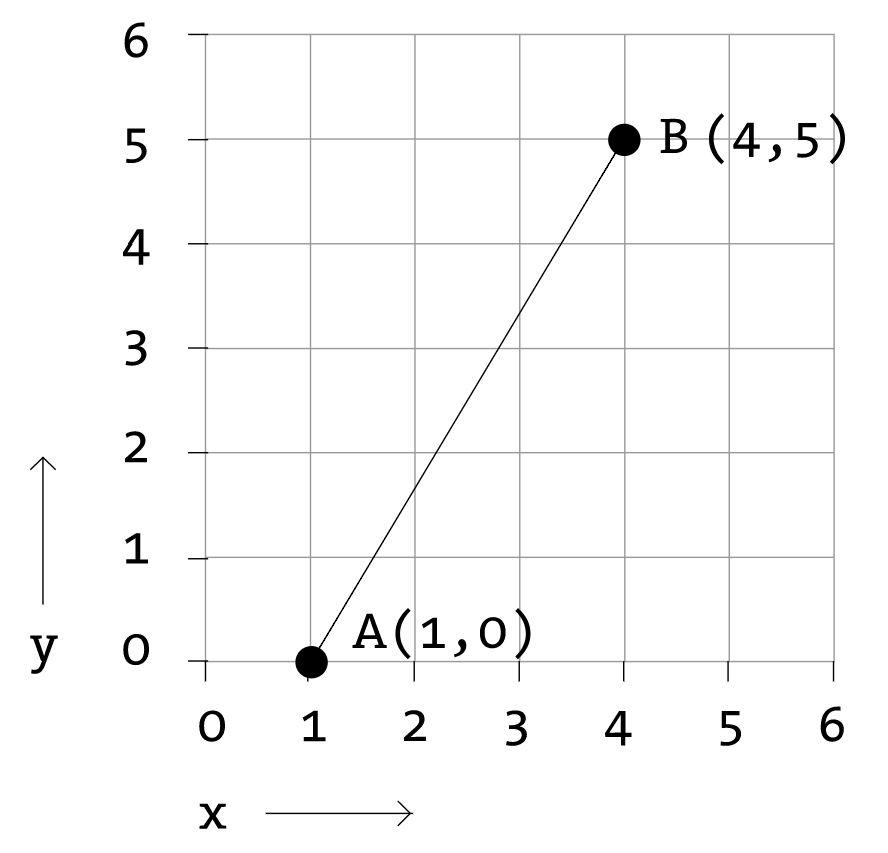
The above figure shows a line between point A (1,0) and point B (4,5). If you wanted to direct a friend of yours to draw that same line, you would give them a shout and say "draw a line from the point one-zero to the point four-five, please." Well, for the moment, imagine your friend was a computer and you wanted to instruct this digital pal to display that same line on its screen. The same command applies (only this time you can skip the pleasantries and you will be required to employ a precise formatting). Here, the instruction will look like this:
line(1,0,4,5);
Even without having studied the syntax of writing code, the above statement should make a fair amount of sense. We are providing a command (which we will refer to as a "function") for the machine to follow entitled "line." In addition, we are specifying some arguments for how that line should be drawn, from point A (1,0) to point B (4,5). If you think of that line of code as a sentence, the function is a verb and the arguments are the objects of the sentence. The code sentence also ends with a semicolon instead of a period.

The key here is to realize that the computer screen is nothing more than a fancier piece of graph paper. Each pixel of the screen is a coordinate - two numbers, an "x" (horizontal) and a "y" (vertical) - that determines the location of a point in space. And it is our job to specify what shapes and colors should appear at these pixel coordinates.
Nevertheless, there is a catch here. The graph paper from eighth grade ("Cartesian coordinate system") placed (0,0) in the center with the y-axis pointing up and the x-axis pointing to the right (in the positive direction, negative down and to the left). The coordinate system for pixels in a computer window, however, is reversed along the y-axis. (0,0) can be found at the top left with the positive direction to the right horizontally and down vertically.

Simple Shapes
The vast majority of p5 programming examples are visual in nature. These examples, at their core, involve drawing shapes and setting pixels. Let's begin by looking at four primitive shapes.
For each shape, we will ask ourselves what information is required to specify the location and size (and later color) of that shape and learn how p5 expects to receive that information. In each of the diagrams below, we'll assume a window with a width of 100 pixels and height of 100 pixels.
A point() is the easiest of the shapes and a good place to start. To draw a point, we only need an x and y coordinate.
A line() isn't terribly difficult either and simply requires two points: (x1,y1) and (x2,y2):
Once we arrive at drawing a rect(), things become a bit more complicated. In p5, a rectangle is specified by the coordinate for the top left corner of the rectangle, as well as its width and height.
A second way to draw a rectangle involves specifying the centerpoint, along with width and height. If we prefer this method, we first indicate that we want to use theCENTER mode before the instruction for the rectangle itself. Note that p5 is case-sensitive.
Finally, we can also draw a rectangle with two points (the top left corner and the bottom right corner). The mode here isCORNERS. Note this example gives the same result on screen as the example above.
Once we have become comfortable with the concept of drawing a rectangle, an ellipse() is a snap. In fact, it is identical to rect() with the difference being that an ellipse is drawn where the bounding box of the rectangle would be. The default mode for ellipse() is CENTER, rather than CORNER.
Now let's look at what some code with shapes in more complete form, with canvas dimensions of 200 by 200. Note the use of the createCanvas() function to specify the width and height of the canvas.
